Calculabilité et décidabilité (Bac 🎯)⚓︎

Ce cours est mis à disposition selon les termes de la Licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.

Sources et crédits pour ce cours
Pour préparer ce cours, j'ai utilisé :
- le manuel NSI et le manuel de MP2I/MPI chez Ellipses de Balabonski, Conchon, Filliâtre, Nguyen pour l'essentiel de la structure et du contenu.
- des articles du site Interstices à propos de la calculabilité :
- série d'articles de Jean-Louis Giavitto sur l'histoire de la définition du calcul dont cet article sur les calculateurs universels
- article de Jean-Gabriel Ganascia sur le lien entre calculabilité et décidabilité
🔖 Synthèse de ce qu'il faut retenir pour le bac
Calculabilité et décidabilité : du programme de Hilbert à la machine universelle de Turing⚓︎
Histoire d'algorithme : des calculus romains à l'Entscheidungsproblem
Le mot calcul vient du latin calculus qui désigne les cailloux utilisés dans les procédures de comptage mécanique pendant l'Antiquité : un caillou pour représenter une unité. Très tôt les hommes ont imaginé des machines capables de réaliser des calculs :
- calculs numériques :
- la machine d'Anticythère (87 av. J.C.) permettait de calculer des positions astronomiques
- la Pascaline inventée par Blaise Pascal au XVIIème siècle, permettait de réaliser des additions et de soustractions
- mais aussi calculs logiques comme l'Ars universalis imaginée par Raymond Lulle au XIIIème siècle, qui par la rotation de deux disques permettait d'énumérer automatiquement toutes sortes de raisonnements plus ou moins obscurs. Au XVIIème Siècle Leibniz imagina le calculus ratiocinator, une machine qui pourrait manipuler des symboles afin de déterminer les valeurs des énoncés mathématiques.

Ars universalis de Raymond Lulle, source : researchgate.net
Définition d'un algorithme
La notion d'algorithme généralise la notion de calcul numérique comme séquence finie de règles bien établies. Un algorithme est une suite finie et non ambiguë d'opérations bien définies qui s'applique à une entrée et produit une sortie, qui apporte une solution à un problème bien spécifié. Le nom algorithme dérive de celui du mathématicien persan Al-Khwarizmi (780 - 850).
Au XIXème siècle, Charles Babbage imagine la machine analytique, précurseur de l'ordinateur moderne avec un système d'entrée, de sortie, une mémoire, un processeur. Ada Lovelace concçoit les ancêtres des premiers programmes informatiques pour cette machine et pointe sa capacité à calculer aussi sur des symboles "La machine peut produire trois types de résultats : (…) symboliques (…) ; numériques (…) ; et algébriques en notation littérale."
En 1900 les mathématiciens réunis en congrès à Paris discutent des fondements logiques qui permettront de construire des mathématiques sûres où tout énoncé bien formulé pourra être soit démontré soit réfuté. Le plus respecté d'entre eux, David Hilbert, affiche un objectif ambitieux : "Wir müssen, wir werden wissen" et présente une liste de problèmes à résoudre pour le siècle à venir : le programme de Hilbert. Le dixième problème touche aux fondements du calcul et des algorithmes puisqu'il consiste à trouver un procédé déterminant automatiquement si une équation diophantienne a des solutions. Cependant, à la même époque, la découverte de certains paradoxes comme celui de Bertrand Russell ébranlent la théorie des ensembles considérée comme un pilier des mathématiques. L'histoire de la quête des fondements des mathématiques, à travers le parcours de Bertrand Russell, est racontée dans le roman graphique culte Logicomix disponible dans toutes les bonnes bibliothèques et CDI.

David Hilbert, source : Wikipedia
En 1928, avec Wilhelm Ackermann, David Hilbert, renouvelle son optimisme dans la conquête des fondements logiques des mathématiques et formule le problème de la décision ou Entscheidungsproblem.
Entscheidungsproblem (Hilbert 1928, version simplifiée)
L'Entscheidungsproblem pose la question suivante : existe-t-il un algorithme qui peut décider si n'importe quel énoncé mathématique bien formulé est vrai ou faux ?
C'est un exemple de problème de décision : sur l'ensemble E des énoncés mathématiques, on considère la fonction f qui à un énoncé e associe True ou False. Le problème est décidable s'il existe un algorithme permettant de calculer f(e) pour tout énoncé e.
En 1929, Kurt Gödel démontre que tout énoncé vrai dans la logique du premier ordre avec symbole d'égalité, peut être démontré. Ce théorème de complétude va dans le sens de Hilbert. Mais en 1931, Kurt Gödel démontre deux théorèmes d'incomplétude qui mettent fin au rêve d'Hilbert. Le premier théorème énonce que dans un système formel, incluant la logique du premier ordre et l'arithmétique des entiers, quels que soient les axiomes qu'on se fixe, il existera toujours des énoncés vrais mais indécidables c'est-à-dire qu'on ne peut pas les démontrer par simple déduction à partir des axiomes. On dit alors que le système est incomplet.
Argument diagonale
Sources : article de Wikipedia et article de Science étonnante sur le théorème d'incomplétude de Gödel
Dans la démonstration de son premier théorème d'incomplétude, Kurt Gödel construit, grâce à un codage astucieux par des entiers, une affirmation équivalente à "Cette affirmation n'est pas démontrable dans ce système". Si elle est fausse alors on peut démontrer une affirmation fausse, cela signifie que le système permet d'énoncer une affirmation vraie (car démontrable) et fausse : on dit que le système est inconsistant. Si elle est vraie alors elle n'est pas démontrable et l'affirmation est indécidable. On en déduit que soit le système est inconsistant, soit il contient une affirmation indécidable. Cet argument d'autoréférence est du même type que celui utilisé par Georg Cantor dans sa preuve de la non dénombrabilité des nombres réels.
si on pouvait numéroter tous les réels par des entiers distincts alors en considérant le développement binaire de chaque entier, on pourrait constuire un réel qui ne serait pas dans l'énumération : il suffirait de prendre sa n-ième décimale différente de la n-ième décimale du n-ième réel de l'énumération : on change les décimales de la diagonale lorsqu'on superpose les réels. On donne ci-dessous une illustration en binaire.

Diagonale de Cantor, source : Wikipedia
Cet argument diagonale ou d'autoréférence, est utilisé aussi par Bertrand Russell dans son paradoxe sur la théorie des ensembles ou par Alan Turing dans sa preuve de l'indécidabilité du problème de l'arrêt. De cette preuve, Turing déduira que l'Entscheidungsproblem est indécidable.
En 1936-1937, Alonzo Church et Alan Turing vont démontrer par deux méthodes différentes que l'Entscheidungsproblem est indécidable.
Décidabilité
Source : article de Jean-Gabriel Ganascia
Une propriété mathématique est décidable s'il existe un algorithme déterminant si elle est vraie ou fausse dans n'importe quel contexte possible. Par exemple, la propriété "être divisible par" est décidable pour tous les couples d'entiers : il existe un algorithme (par soustractions successives du diviseur), pour déterminer si un entier A est divisible par un entier B.
L'Entscheidungsproblem pose la question de la décidabilité d'une propriété, c'est un problème de décision.
Naissance de l'informatique moderne : des modèles de calcul aux machines universelles
En 1936, Alonzo Church et Alan Turing ont démontré de façon indépendante que l'Entscheidungsproblem est indécidable : il ne peut exister d'algorithme capable de déterminer si n'importe quel énoncé mathématique bien formulé est vrai ou faux.
Pour obtenir ce résultat, ils ont développé des modèles théoriques recouvrant ce qu'on désigne intuitivement par calcul ou plus généralement algorithme : un nombre fini d'opérations bien définies qui s'applique à une entrée pour produire une sortie qui est la solution d'un problème. Turing a conçu un modèle fondé sur des machines théoriques et Church sur un langage formel appelé lambda-calcul. Par ailleurs, Stephen Kleene, thésard de Church, a développé au même moment un modèle de calcul de fonctions récursives définies à partir de 6 schémas de base.
De plus Turing et Kleene ont démontré en 1937 que les fonctions calculables par une machine de Turing sont les mêmes que celles calculables par le lambda-calcul ou les fonctions récursives de Kleene.
La thèse de Church-Turing est une conjecture (donc non démontrée) qui affirme que la notion intuitive de calcul est entièrement capturée par ces modèles de calcul équivalents de Turing, Church et Kleene.
Calculabilité
Une fonction calculable est une fonction mathématique \(f\) définie sur un ensemble E pour laquelle il existe un algorithme (ou une machine de Turing d'après la thèse de Church-Turing) qui pour tout \(x\) appartenant à E, calcule son image \(y=f(x)\) par \(f\) en un temps fini.
On est habitué en mathématique à manipuler des fonctions calculables, pourtant on peut démontrer qu'il existe une infinité dénombrable de fonctions calculables (car un algorithme comporte un nombre fini de caractères) mais une infinité non dénombrable de fonctions non calculables (donc plus de fonctions non calculables que calculables au sens des infinis de Cantor). Un exemple historique de fonction non calculable est la fonction arret qui prend en argument un algorithme f et une entrée e et arret(f, e) renvoie True si f(e) se termine et False sinon. Alan Turing a démontré qu'elle est non calculable.
Une fonction calculable qui prend ses valeurs dans l'ensemble des booléens est dite décidable. Alan Turing a donc démontré que la fonction de l'arrêt est non décidable. On parle plutôt de problème non décidable.
Par un procédé appelé réduction, il a ensuite démontré que l'indécidabilité du problème de l'arrêt entraîne l'indécidabilité de l'Entscheidungsproblem.

Alan Turing, source : Wikipedia
Machines de Turing et machine universelle
Source : articles de Jean-Louis Giavitto Sous le signe du calcul et Des calculateurs universels
Une machine de Turing permet de modéliser un algorithme. On peut distinguer deux parties :
- la partie données :
- une tête peut se déplacer le long d'un ruban potentiellement infini, sur lequel elle peut lire ou écrire des symboles pris dans un alphabet fini.
- la partie contrôle :
- la machine possède un état interne et l'ensemble des états internes possibles est fini
- quand la tête lit un symbole, selon l'état interne, elle peut éventuellement modifier le symbole et se déplacer vers la droite ou la gauche du symbole courant sur le ruban.
Si on change d'algorithme il faut donc une nouvelle machine de Turing.
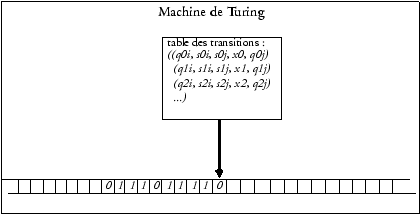
Machine de Turing, source : https://www.laurentbloch.org
Alan Turing a cependant réalisé le tour de force de démontrer qu'on peut construire une machine de Turing universelle. Celle-ci peut prendre en entrée sur son ruban la description d'une machine de Turing particulière M ainsi que son entrée E et peut alors simuler l'exécution de M sur En pour écrire en sortie sur son ruban le même résultat que si M s'était appliquée à E.
Dans une machine de Turing universelle, un algorithme (\(=\) une machine de Turing particulière) est traité comme une donnée. Ainsi une seule machine peut exécuter tous les algorithmes (\(=\) fonctions calculables) et les algorithmes sont codés dans la machine sous forme de programmes.
Les ordinateurs et ordiphones que nous connaissons sont des machines de Turing universelles. Il sont basés sur l'architecture de Von Neumann où la mémoire contient les programmes et les données comme le ruban d'une machine de Turing universelle.
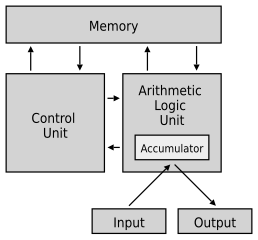
Architecture de Von Neumann, source : Wikipedia
Langages de programmation Turing complets
Pour faire exécuter un algorithme à une machine de Turing universelle, on doit coder l'algorithme sur le ruban comme une donnée à l'aide d'un alphabet fini de symboles. Lorsque les machines de Turing universelles ont été réalisées sous forme d'ordinateurs, ce codage de l'algorithme comme donnée de la machine s'est appelé l'implémentation de l'algorithme dans un langage de programmation.
Les langages de programmation qui permettent d'exprimer toutes les machines de Turing, c'est-à-dire tous les algorithmes calculables au sens de la thèse de Church-Turing, sont dits Turing complets.
Exercice 2 : fonctionnement d'une machine de Turing
On considère la machine de Turing décrite ci-dessous avec son entrée et la table de transitions décrivant l'évolution de l'état interne et l'action de la tête de lecture/écriture en fonction du symbole lu et de l'état courant.

Cette machine modélise l'algorithme qui ajoute 1 à son entrée.
Décrire avec crayon et papier l'évolution du ruban et de la tête de lecture au cours de l'exécution de l'algorithme puis vérifier en exécutant le simulateur de la page https://interstices.info/comment-fonctionne-une-machine-de-turing/.
Exercice 3 : lambda-calcul en Python avec les fonctions anonymes lambda
Source : le manuel NSI et le manuel de MP2I/MPI chez Ellipses de Balabonski, Conchon, Filliâtre, Nguyen
D'après la thèse de Church-Turing, les fonctions calculables couvrent tout ce qui peut être calculable. Dans son modèle du lambda-calcul, Alonzo Church définit une fonction calculable comme une fonction dont le résultat est obtenu par une combinaison de fonctions calculables. En lambda-calcul on distingue :
- les variables : x, y... qui sont des lambda-termes ;
- les applications : u v est un lambda-terme si u et v sont des lambda-termes ;
- les abstractions qui formalisent les fonctions : λx.v est un lambda-terme si x est une variable et v un lambda-terme.

Alonzo Church, source https://comentariosdemislibrosfavoritos.blogspot.com
En Python, on peut écrire des fonctions à la manière du lambda-calcul avec une fonction anonyme lambda.
On donne quelques exemples :
| Fonction mathématique | En lambda-calcul | En Python | Application en mathématiques | Application en lambda-calcul | Application en Python |
|---|---|---|---|---|---|
| Fonction affine \(f:x \mapsto x + 4\) | λx.x+4 | lambda x: x + 4 |
\(f(3)=3+4=7\) | (λx.x+4)(3)=4+3=7 | (lambda x: x + 4)(3) |
| Composée de fonctions \(g \circ f: x \mapsto g(f(x))\) | λf.λg.λx.(g(f(x))) | lambda f: lambda g: lambda x: g(f(x)) |
Composée de \(f:z \mapsto z + 5\) suivie de \(g:y \mapsto 4*y\) | λf.λg.λx.(g(f(x)))(λy.(4*y))(λz.z+5)=λx.(4*(x+5)) | (lambda f: lambda g: lambda x: g(f(x)))(lambda z: z+5)(lambda y: 4*y) |
Question 1
On a implémenté les fonctions décrites dans le tableau précédent dans l'éditeur ci-dessus.
- Sans utiliser Python, déterminer la valeur de
compose(f1)(g1)(6). Vérifier avec Python - Écrire la fonction carré \(f:x \mapsto x * x\) en lambda-calcul (on suppose la multiplication disponible) puis en Python avec une fonction anonyme
lambda.
compose(f1)(g1)(6)vaut \(4(6 + 5)=44\).- La fonction carré \(f:x \mapsto x * x\) s'écrit (λx.(x*x) en lambda-calcul et
lambda x: x * xen Python.
Question 2
En lambda-calcul, les fonctions sont anonymes donc, sans nom, comment peut-on définir une fonction récursive qui fait référence à elle-même ?
La solution est fournie par la fonction dite de combinateur de point fixe. Si on la note \(Z\), on a pour tout lambda-terme v auquel elle s'applique : e Zg=g(Zg). Le lambda-terme Zg est ainsi un point fixe du lmabda-terme g. En Python on explicite l'argument de la fonction Zg avec le combinateur défini par Zgv=g(Zg)v sinon l'évaluation de Zg est infinie (caractéristique des langages de programmation stricts qui forcent l'évaluation complète des arguments lors de l'appel d'une fonction, voir l'article Wikipedia).
Armé du combinateur de point fixe, on peut représenter en lambda-calcul des fonctions récursives et donc des boucles.
Dans l'éditeur ci-dessus on fournit un exemple de représentation en Python, à la manière du lambda-calcul de la fonction récursive renvoyant le \(n_{eme}\) nombre triangulaire : \(\begin{cases}t_{0}= 0 \\ t_{n}=n + t_{n-1} \quad \mathrm{ si } \quad n \geqslant 1 \end{cases}\).
Sur le modèle de la fonction triangulaire, écrire à la manière du lambda-calcul, une fonction récursive factorielle qui prend en argument un entier naturel \(n\) et renvoie \(n!=\prod_{k=1}^{n}k\) avec la convention que \(0!=1\).
factorielle = fixed_point_combinator(lambda f: lambda n: 1 if n == 0 else n * f(n - 1))
Modèles de calcul et paradigmes de programmation
Le modèle de calcul des machines de Turing est à l'origine des langages de programmation du paradigme impératif comme le langage C, alors que le modèle du lambda-calcul se retrouve dans les langages du paradigme fonctionnel comme Ocaml. On peut considérer que Python s'il s'utilise dans un style impératif dans la majorité des cas, possède des traits de langage fonctionnel. On parle de langage multiparadigme.